Cohomology of finitely presented groups

Peter Michael Curran

Vol. 42 (1972), No. 3, 615–620

DOI: 10.2140/pjm.1972.42.615

Abstract

Let G be a finitely presented group, G′ a finite quotient of G and K a field. Let G act on the group algebra V = K[G′] in the natural way. For a suitable choice of G′ we obtain estimates on the dimension of H¹(G,V ) in terms of the presentation and then use these estimates to derive information about G.

If G is generated by n elements, of which m have finite orders k₁,⋯,k_m, resp., and G has the presentation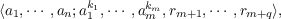

then, in particular, we show that (a) the minimum number of generators of G is ≧n−q −∑ 1∕k_i; (b) if this lower bound is actually attained, then G is free, of this rank, and (c) G is infinite if ∑ 1∕k_i ≦n−q − 1. The latter, together with a result of R. Fox, yields an algebraic proof that the group

is infinite if ∑ 1∕k_i ≦ m − 2.

Mathematical Subject Classification 2000

Primary: 20F05

Secondary: 18H10

Milestones

Received: 27 May 1970

Revised: 21 July 1972

Published: 1 September 1972