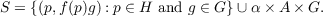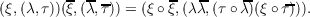Automorphisms on cylindrical semigroups

Joan Geramita

Vol. 43 (1972), No. 1, 93–105

DOI: 10.2140/pjm.1972.43.93

Abstract

This paper characterizes the automorphisms of a cylindrical semigroup S in terms of the automorphisms of the defining subgroups and subsemigroups. The following theorem is representative of the type of information given in this paper.

Let F : R → A be a dense homomorphism of the additive real numbers to the compact abelian group A. Let λ be a positive real number. Multiplication by λ shall also denote the automorphism of A whose restriction to F(R) is given by FλF⁻¹. The set of all such λ for a given F is called Λ_1^Γ.

Theorem. Let f and λ be as above. Let G be a compact group. Let

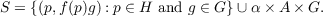
Then α;S → S is an automorphism if and only if α(p,f(p),g) = (λp,f(λp),τ(f(p))ξ(g));α(∞,a,g) = (∞,λa,τ(a)ξ(g)), where τ : A → G is a homomorphism into the centre of G and, ξ : G → G is an automorphism. Theorem. Let S be as in theorem above. Let 𝒜(G) be the automorphism group of G, and Z(G), the center of G. The automorphism group of S is isomorphic as an abstract group to 𝒜(G) × (A_F × Hom(A,Z(G))) with the following multiplication

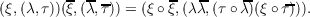
Mathematical Subject Classification 2000

Primary: 22A15

Milestones

Received: 15 July 1971

Revised: 28 September 1971

Published: 1 October 1972