|
|||||

|

|
|

|

|
|
Distributing tensor
product over direct product
Kenneth R. Goodearl |
|
Vol. 43 (1972), No. 1, 107–110
|
Abstract |
|
This paper is an investigation of conditions on a module A under which the natural map 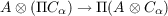 is an injection. The investigation leads to a theorem that a commutative von Neumann regular ring is self-injective if and only if the natural map 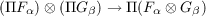 is an injection for all collections {Fα} and {Gβ} of free modules. An example is constructed of a commutative ring R for which the natural map ![R[[s]]⊗R [[t]] → R[[s,t]]](a112x.png) is not an injection. |
Mathematical Subject Classification
Primary: 16A50
|
Milestones
Received: 28 July 1971
Published: 1 October 1972
|
Authors |
| Kenneth R. Goodearl | |
| University of California, Santa
Barbara Santa Barbara CA United States |
|
 |
