Weighted convergence in length

William Richard Derrick

Vol. 43 (1972), No. 2, 307–315

DOI: 10.2140/pjm.1972.43.307

Abstract

This paper studies the lower semicontinuity of weighted length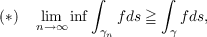

where the sequence of curves {γ_n} converges uniformly to the curve γ, and f is a nonnegative lower semicontinuous function. Necessary and sufficient conditions for equality in (∗) are obtained, as well as conditions which prevent γ from being rectifiable. Requirements are given for the attainment of the weighted distance, from a point to a set, and the families of functions, for which weighted distance is attained or (∗) is satisfied, are shown to be monotone closed from below. Finally, the solutions to the integral inequality

are shown to be compact if the initial values γ(0) lie in a compact set.

Mathematical Subject Classification 2000

Primary: 28A75

Milestones

Received: 10 May 1971

Revised: 20 July 1971

Published: 1 November 1972