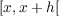|
A reformulation of
the Krein-Milman Theorem is used to obtain an integral representation of
each function in a certain class of real monotonic functions defined on [0,1].
Let {i1,i2,is,⋯} denote a fixed sequence all of whose terms are either 0
or 1, and let M1 be the set of real nonnegative functions f on [0,1] such
that
![(− 1)(i1)Δ1hf(x) = (− 1)(i1)[f(x+ h)− f (x)] ≧ 0,](a160x.png)
h > 0, for  ⊂ [0,1]. Let Mn,n > 1, be the set of functions belonging to
Mn−1 such that
![(− 1)(in)Δnhf(x) = (− 1)(in)[Δnh−1f(it+ h)− Δnh−1f(x )] ≧ 0](a162x.png)
for [x,x + nh] ⊂ [0,1]. If f ∈ Mn, then f is said to be an n-monotone function. Since
the sum of two n-monotone functions is in Mn and since a nonnegative real
multiple of an n-monotone function is an n-monotone function, the set Mn is a
convex cone. It is the purpose of this paper to give the extremal elements
(i.e., the generators of extreme rays) of this cone, and to show that for the
n-monotone functions an integral representation in terms of extremal elements is
possible.
|
