Invariant functions of an iterative process for maximization of a polynomial

Peter F. Stebe

Vol. 43 (1972), No. 3, 765–783

DOI: 10.2140/pjm.1972.43.765

Abstract

Let P be a polynomial with real non-negative coefficients and variables x_ij,i = 1,⋯,k,j = 1,⋯,n_i. Let d = ∑ ^k1n_i. Let R_d be the d-dimensional real vector space. Let M be the subset of R_d defined by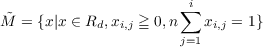

where the symbols x_i,j denote the components of x. If x is a vector in the interior of M, define τ(x) as the vector in M with components x_i,j′ given by

The expression on the right is evaluated at x. The transformation τ is defined on the boundary of M by the same formula if the denominators do not vanish.

Let F be the set of fixed points of τ in M. It is shown that if τ is a homeomorphism of M onto itself, there is a set of d−k functions f₁,⋯ , f_d−k defined on M−F such that f_i(x) = f_i(τ(x)) for x ∈M−F. The functions f_i are continuous and independent on an open dense subset of M−F. Explicit expressions for certain invariant functions are also obtained.

Mathematical Subject Classification 2000

Primary: 58E15

Secondary: 54H15

Milestones

Received: 18 February 1971

Revised: 20 July 1972

Published: 1 December 1972