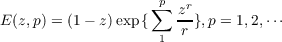|
In the theory of integral
functions, the expressions
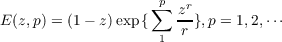 | (1) |
called primary factors, are of some importance, and it is of interest to find upper
bounds for |E(z,p)|. Clearly E(z,p) = 0 only for z = 1, and so for other values,
define f(z,p) = log |E(z,p)|. It is known that for suitable constants ap,bp the
inequalities
| f(z,p) | ≦ ap|z|p,|z|≧ 1,z≠1 | (2)
| | f(z,p) | ≦ bp|z|p+1,|z|≦ 1,z≠1 | (3) |
are satisfied; for instance Hille has shown that one may take ap = 1+∑
1p1∕r ≦ 2+log p
and bp = 1.
In this paper, the smallest values of both ap and bp are determined, the latter in
closed form.
|