Differential inequalities and local valency

Walter Kurt Hayman

Vol. 44 (1973), No. 1, 117–137

DOI: 10.2140/pjm.1973.44.117

Abstract

An entire function f(z) is said to have bounded value distribution (b.v.d.) if there exist constants p,R such that the equation f(z) = w never has more than p roots in any disk of radius R. It is shown that this is the case for a particular p and some R > 0 if and only if there is a constant C > 0 such that for all z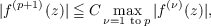

so that f′(z) has bounded index in the sense of Lepson.

Mathematical Subject Classification 2000

Primary: 30A32

Secondary: 34A40, 34C10, 30A66

Milestones

Received: 27 August 1971

Published: 1 January 1973