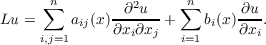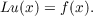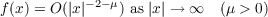Bounded entire solutions of elliptic equations

Avner Friedman

Vol. 44 (1973), No. 2, 497–507

DOI: 10.2140/pjm.1973.44.497

Abstract

Let

(1.1)

Consider the equation

(1.2)

It is shown, under some general conditions on the coefficients of L, that if f(x) is locally Hölder continuous and

(1.3)

then there exists a bounded solution of (1.2) in Rⁿ when n ≧ 3. If n = 2 then bounded entire solutions may not exist, but there exists a nonnegative solution of (1.2) in R² which is bounded above by 0(log |x|). An application of these results to the Cauchy problem is given in the final section of the paper.

Mathematical Subject Classification 2000

Primary: 35J15

Milestones

Received: 15 October 1971

Published: 1 February 1973