Extensions of inequalities of the Laguerre and Turán type

Merrell Lee Patrick

Vol. 44 (1973), No. 2, 675–682

DOI: 10.2140/pjm.1973.44.675

Abstract

It is shown that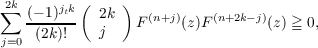

for −∞ < z < ∞,n ≧ 1 and k ≧ 0, where F(z) is an entire function of a special type. For k = 1 this simply is the well known Laguerre inequality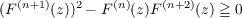

−∞ < z < ∞,n ≧ 0. From these inequalities we obtain the inequalities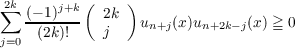

which hold for such values of x, for which the functions u_n = u_n(x) have a generating function of the type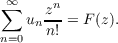

Mathematical Subject Classification

Primary: 33A70

Secondary: 30A66

Milestones

Received: 4 October 1971

Published: 1 February 1973