On groups of exponent four satisfying an Engel condition

R. B. Quintana and Charles R. B. Wright

Vol. 44 (1973), No. 2, 701–705

DOI: 10.2140/pjm.1973.44.701

Abstract

Let B(n) be the Burnside (i.e., freest) group of exponent 4 on n generators. It is known that B(n) is nilpotent of class at most 3n − 1. This paper exhibits a commutator of length 3n − 1 in B(n) which must be nontrivial if the class is exactly 3n − 1. The methods also yield an easy proof of the following.

Theorem. Let E(n) be B(n) reduced modulo the identical commutator relation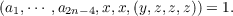

Then E(n) is nilpotent of class at most 2n + 3.

As an immediate corollary, every n-generator group of exponent 4 satisfying the Engel condition (x,y,y,y) = 1 identically is of class at most 2n + 3.

Mathematical Subject Classification 2000

Primary: 20F45

Milestones

Received: 1 October 1971

Revised: 10 January 1972

Published: 1 February 1973