Enumeration of up-down permutations by number of rises

Recent Issues

Vol. 322: 1 2

Vol. 321: 1 2

Vol. 320: 1 2

Vol. 319: 1 2

Vol. 318: 1 2

Vol. 317: 1 2

Vol. 316: 1 2

Vol. 315: 1 2

Online Archive

Volume:

Issue:

The Journal

ISSN: 1945-5844 (e-only)

ISSN: 0030-8730 (print)

Vol. 45 (1973), No. 1, 49–58

DOI: 10.2140/pjm.1973.45.49

It is well known that A(n), the number of up-down permutations of {1,2,⋯,n} satisfies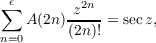

∑𝜖 -z2n- A(2n)(2n)! = secz, n=0

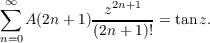∑∞ z2n+1 A(2n+ 1)(2n+-1)! = tanz. n=0

In the present paper generating functions are obtained for the number of up-down permutations counting the number of rises among the “peaks”.

Primary: 05A15

Received: 17 November 1971

Published: 1 March 1973