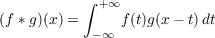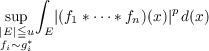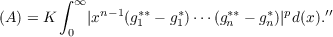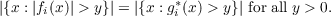Two-sided L_p estimates of convolution transforms

Gary Sampson

Vol. 45 (1973), No. 1, 347–356

DOI: 10.2140/pjm.1973.45.347

Abstract

Let f and g be two Lebesgue measurable functions on the real line. Then the equation

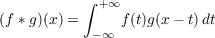
defines the convolution transform of f and g. In an earlier paper [4] we obtained sharp upper and lower eetimates for the expression

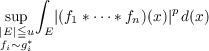(A)

where p = 1,2 and 4, with applications to Fourier transform inequalities. This paper contains estimates of (A) for all values of p(p ≧ 1) in the case where E = (−∞,+∞). For example, one of our theorems implies the following:

“If g_i^∗ is bounded and has compact support for all i, then there exists a constant K,1∕(p + 1)^p ≦ K ≦ (p′ + 1)^p(2ⁿ⁻¹)^p, such that

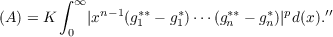
Here g_i^∗ are preassigned decreasing functions and the symbol f_i ∼ g_i^∗ means

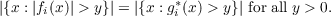
Mathematical Subject Classification 2000

Primary: 44A35

Milestones

Received: 26 July 1971

Published: 1 March 1973