On the rest points of a nonlinear nonexpansive semigroup

Chi-Lin Yen

Vol. 45 (1973), No. 2, 699–706

DOI: 10.2140/pjm.1973.45.699

Abstract

Let X be a reflexive Banach space and T a nonlinear nonexpansive semigroup on X. The results which we shall prove are the following:

Theorem 1. Suppose that for any closed convex set M with the property that T(t)M ⊆ M for all t ≥ 0,M contains a precompact orbit. Then T has a rest point. Moreover, the set of all rest points of T is connected.

Theorem 2. Suppose that X is strictly convex and T has a bounded orbit. If there is an unbounded increasing sequence {u_i} of positive numbers and point x such that lim_i→∞T(u_i)x exists then T has a rest point. Moreover, if {t_i} is an unbounded increasing sequence of positive numbers such that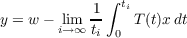

exists, then y ∈ F.

Mathematical Subject Classification 2000

Primary: 47H99

Milestones

Received: 24 November 1971

Published: 1 April 1973