|
|||||

|

|
|

|

|
|
Length of period simple
continued fraction expansion of √d
Dean Robert Hickerson |
|
Vol. 46 (1973), No. 2, 429–432
|
Abstract |
|
In this article, the length,
p(d), of the period of the simple continued fraction (s.c.f.) for 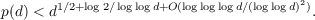 In addition, some properties of the complete quotients of the s.c.f. expansion of |
Mathematical Subject Classification
Primary: 10F20
|
Milestones
Received: 28 April 1972
Published: 1 June 1973
|
Authors |
| Dean Robert Hickerson | |
 |
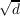 is discussed,
where
is discussed,
where 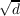 are developed.
are developed.