On the number of polynomials of an idempotent algebra. II

George Grätzer and J. Płonka

Vol. 47 (1973), No. 1, 99–113

DOI: 10.2140/pjm.1973.47.99

Abstract

In part I of this paper a conjecture was formulated according to which, with a few obvious exceptions, the sequence ⟨p_n(U)⟩ of an idempotent algebra is eventually strictly increasing. In this paper this conjecture is verified for idempotent algebras satisfying p₂(U) = 0,p_a(U) > 0, and p₄(U) > 0. In fact, somewhat more is proved:

Theorem. Let U be an idempotent algebra with no essentially binary polynomial and with essentially ternary and quaternary polynomials. Then the sequence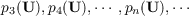

is strictly increasing, that is, for all n ≧ 2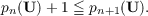

Mathematical Subject Classification

Primary: 08A25

Milestones

Received: 6 May 1972

Published: 1 July 1973