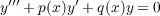An asymptotic property of solutions of y′′′ + py^′ + qy = 0

Gary Douglas Jones

Vol. 47 (1973), No. 1, 135–138

DOI: 10.2140/pjm.1973.47.135

Abstract

In this paper, the differential equation

(1)

will be studied subject to the conditions that p(x) ≦ 0,q(x) > 0, and p(x),p′(x), and q(x) are continuous for x ∈ [0,+∞). A solution of (1) will be said to be oscillatory if it changes signs for arbitrarily large values of x. It will be shown that if (1) has an oscillatory solution then every nonoscillatory solution tends to zero as x tends to infinity.

Mathematical Subject Classification 2000

Primary: 34C10

Milestones

Received: 23 March 1972

Published: 1 July 1973