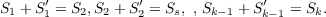|
Let the reverse of any positive
integer N be N′ and N + NJ = S1. Then
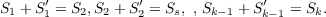
Each of the Si, the result of a reversal-addition operation on an integer, can
appropriately be called a versum (a term coined in 1965 by Michael T. Rebmann and
Frederick Groat while undergraduates at Carleton College). Thus, reiteration of the
operation generates a sequence of versums. An ancient conjecture says that for every
N there is a palindromic Sk. True for one-digit and two-digit N’s in the decimal
system, considerable doubt has been thrown upon the universal verity of the
conjecture [1, 2].
In the binary system, D. C. Duncan disproved the conjecture by a counter-example
in which the sequence exhibits a palindrome-free recursive cycle of four versums
(hereafter referred to as a PFRC-4). Sprague, Gabai and Coogan, and Brousseau
rediscovered the same cycle. Brousseau also found two other palindrome-free
sequences, each with a different PFRC-4.
Duncan remarked that “it would be highly interesting to establish the
existence of numbers that neither become palindromic nor show a periodic
recursion of cycles of digits.” Such integers are reported below, together with an
unlimited number of distinct palindrome-free recursive cycles in the binary
system.
|