Differentiable open maps of (p + 1)-manifold to p-manifold

Philip Throop Church and James Timourian

Vol. 48 (1973), No. 1, 35–45

DOI: 10.2140/pjm.1973.48.35

Abstract

Let f : M^p+1 → N^p be a C⁸ open map with p ≧ 1, let R_p−1(f) be the critical set of f, and let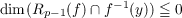

for each y ∈ Np. Then (1.1) there is a closed set X ⊂ M^p+1 such that dimf(X) ≦ p− 2 and, for every x ∈ M^p+1 −X, there is a natural number d(x) with f at x locally topologically equivalent to the map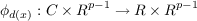

defined by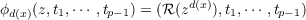

(ℛ(z^d(x)) is the real part of the complex number z^d(x)).

Mathematical Subject Classification

Primary: 57D35

Milestones

Received: 21 June 1972

Published: 1 September 1973