Ergodicity in von Neumann algebras

Charles Radin

Vol. 48 (1973), No. 1, 235–239

DOI: 10.2140/pjm.1973.48.235

Abstract

We investigate the ergodicity of elements of a von Neumann algebra A under the action of an arbitrary cyclic group of inner ∗-automorphisms of U. A simple corollary of our results is the following characterization: A von Neumann algebra A is finite if and only if for each A ∈ U and inner ∗-automorphism α of A, there exists A ∈ A such that 1∕N ∑ _n=0^N−1αⁿ(A)−→A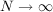

in the weak operator topology.

Mathematical Subject Classification 2000

Primary: 46L10

Milestones

Received: 6 June 1972

Published: 1 September 1973