Existence of Dirichlet finite biharmonic functions on the Poincaré 3-ball

Leo Sario and Cecilia Wang

Vol. 48 (1973), No. 1, 267–274

DOI: 10.2140/pjm.1973.48.267

Abstract

In an earlier study we discussed the existence of quasiharmonic functions, i.e., solutions of Δu = 1. We showed, in particular, that there exist Dirichlet finite quasiharmonic functions on the Poincaré 3-ball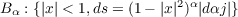

if and only if α ∈ (−3∕5,1). We now ask: Is the existence of these functions entailed by that of Dirichlet biharmonic functions? This is known to be the case for dimension 2. We shall show that, perhaps somewhat unexpectedly, it is no longer true for dimension 3.

Mathematical Subject Classification 2000

Primary: 53C20

Secondary: 31B30

Milestones

Received: 19 July 1972

Published: 1 September 1973