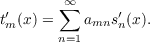|
Let f be L-integrable and
periodic with period 2π, and let
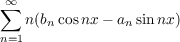 | (1.1) |
be the derived Fourier series of the function f with partial sums sn′(x). We
write
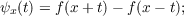
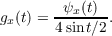
In this paper, the following theorems are established.
Theorem 1. Let A = (amn) be a regular infinite matrix of real numbers. Then, for
every x ∈ [−π,π] for which gx(t) is of bounded variation on [0,π],
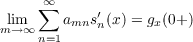 | (1.2) |
if and only if
![∞∑
lim amnsin(n + 1∕2)t = 0 for all t ∈ [0,π].
m→ ∞n=1](a144x.png) | (1.3) |
Theorem 2. Let A = (amn) be an almost regular infinite matrix of real
numbers. Then, for each x ∈ [−π,π] for which gx(t) is of bounded variation on
[0,π],
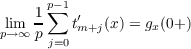
uniformly in m if and only if
![1p∑−1 ∞∑
lp→im∞ p am+j,n sin(n+ 1∕2)t = 0 for all t ∈ [0,π],
j=0n=1](a146x.png)
uniformly in m, where
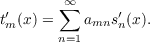
|





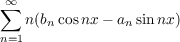
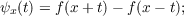
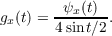
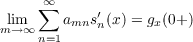
![∞∑
lim amnsin(n + 1∕2)t = 0 for all t ∈ [0,π].
m→ ∞n=1](a144x.png)
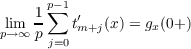
![1p∑−1 ∞∑
lp→im∞ p am+j,n sin(n+ 1∕2)t = 0 for all t ∈ [0,π],
j=0n=1](a146x.png)