On dominant and codominant dimension of QF − 3 rings

David A. Hill

Vol. 49 (1973), No. 1, 93–99

DOI: 10.2140/pjm.1973.49.93

Abstract

In this paper the concept of codominant dimension is defined and studied for modules over a ring. When the ring R is artinian, a left R module M has codominant dimension at least n in case there exists a projective resolution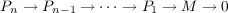

with P_i injective. It is proved that every left R-module has the above property if and only if R has dominant dimension at least n. The concept of codominant dimension is also used to study semi-perfect QF − 3 rings.

Mathematical Subject Classification

Primary: 16A36

Milestones

Received: 8 February 1972

Revised: 3 June 1973

Published: 1 November 1973