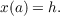|
Consider the integro-differential
equation
![∫
′ t
U (x ) ≡ x + A(t,x )+ a F(t,s,x(s)) ds = T(t),t ∈ [a,b]](a120x.png) | (*) |
subject to the initial condition
 | (**) |
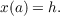Then a problem in approximation theory is whether a solution x(t) of ((∗),(∗∗))
can be approximated, uniformly on [a,b], by a sequence of polynomials Pn, which
satisfy (∗) and minimize the expression ||T(⋅) −U(Pn)∥, where ∥⋅∥ is a certain norm.
It is shown here that such a sequence of minimizing polynomials, or, more generally,
hyperpolynomials, exists with respect to the Lp-norm (1 < p ≦∞) and converges to
x(t), uniformly on [a,b], under the mere assumption of existence and uniqueness of
x(t).
|
