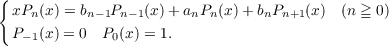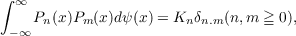|
Let {an}n=0∞ and {bn}n=0∞
be real sequences with bn > 0 and {bn}n=0∞ bounded. Let {Pn(x)}n=0∞ be a
sequence of polynomials satisfying the recurrence formula
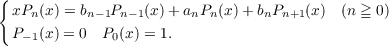 | (1.1) |
Then there is a substantially unique distribution function ψ(t) with respect to which
the Pn(x) are orthogonal. That is,
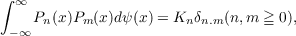
where Kn≠0 and δn,m is the kronecker delta. This paper gives a method of
constructing ψ(x) for the case limn→∞b2n = 0, limn→∞b2n+1 = b < ∞, the set of
limit points of {αn}n=1∞ equals {−α,α} and limn→∞{a2n + a2n+1} = 0. The same
method can be used in the case limn→∞bn = 0 and the set of limit points of
{an}n=0∞ is bounded and finite in number.
|