|
Let G be a locally compact
group, p a number in 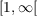 , and Lp the usual Lp-space with respect to left Haar
measure on G. The space Lpt consists of those functions f in Lpt such that g ∗ f is
well-defined and in Lp for each g in Lp. Since each function in Lpt may be identified
with a linear operator on Lp which, as it turns out, is bounded; the operator norm
may be super-imposed on Lpt and, under this norm ∥∥pt,Lpt is a normed algebra.
The family of right multipliers (i.e., bounded linear operators which commute with
left multiplication operators) on any normed algebra A will be written as mr(A) and
the family of left multipliers as m1(A). The family of all bounded linear
operators on Lp which commute with left translations will be written as
Mp. , and Lp the usual Lp-space with respect to left Haar
measure on G. The space Lpt consists of those functions f in Lpt such that g ∗ f is
well-defined and in Lp for each g in Lp. Since each function in Lpt may be identified
with a linear operator on Lp which, as it turns out, is bounded; the operator norm
may be super-imposed on Lpt and, under this norm ∥∥pt,Lpt is a normed algebra.
The family of right multipliers (i.e., bounded linear operators which commute with
left multiplication operators) on any normed algebra A will be written as mr(A) and
the family of left multipliers as m1(A). The family of all bounded linear
operators on Lp which commute with left translations will be written as
Mp.
It was shown in a previous issue of this journal that the Banach algebra Mp is
linearly isomorphic to the normed algebra mr(Lpt), whenever the group G is either
Abelian or compact. This fact is shown, in the present paper, to hold for general
locally compact G. The norm ∥∥pt is defective in that, unless p = 1,(Lpt,∥∥pt) is
never complete.
An attempt will be made in the sequel to supply this deficiency by the
introduction of a second norm ∥|∥|pt on Lpt under which Lpt is always a Banach
algebra. It will be seen that, for p = 2 (and of course for p = 1), the Banach algebra
mr(Lpt,∥|∥|pt) is linearly isometric to Rlp.
|





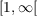 , and
, and 