|
Let C(X) and C(Y ) be the
supremum normed Banach spaces of continuous complex valued functions on the
compact Hausdorff spaces X and Y respectively. Let A and B be closed
subspaces of C(X) and C(Y ) respectively. A map from A to B will mean a
continuous invertible linear map of A to B. The set of all such maps will
be denoted by L(A,B). For T in L(A,B) define c(T) = 1∕(∥T∥∥T−1∥). A
generalization of the Banach-Stone theorem is proved which shows that
there is a constant d < 1 such that if A and B satisfy certain additional
technical restrictions and there is a T in L(A,B) with c(T) > d then X and
Y are homeomorphic. Furthermore, T is, roughly, composition with this
homeomorphism.
For S a connected subset of C bounded by a finite number of disjoint Jordan
curves, denote by A(S) the Banach space of functions in C(S) which are analytic on
the interior of S. For two such domains, S and S′, set d(S,S′) = inf 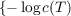 ;T a
linear map of A(S) onto ;T a
linear map of A(S) onto 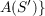 . By analyzing maps T for which c(T) is nearly one,
it is shown that d(⋅,⋅) is a metric on the space of moduli of such domain
(considered as Riemann surfaces) and that this metric induces the classical moduli
topology. . By analyzing maps T for which c(T) is nearly one,
it is shown that d(⋅,⋅) is a metric on the space of moduli of such domain
(considered as Riemann surfaces) and that this metric induces the classical moduli
topology.
|





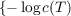
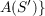 . By analyzing maps
. By analyzing maps 