|
Recently, Joseph D. E.
Konhauser discussed two polynomial sets {Y nα(x;k)} and {Znα(x;k)},
which are biorthogonal with respect to the weight function xαe−x over the
interval (0,∞), where α > −1 and k is a positive integer. For the polynomials
Y nα(x;k), the following bilateral generating function is derived in this paper:
![∑∞ α n − (α+1)∕k −1∕k
Yn (x;k )ζn(y)t = (1− t) exp{x[1 − (1 − t) ]}
n=0
⋅G [x(1 − t)−1∕k,yt∕(1− t)],](a210x.png) |
(1)
|
where
![∑∞
G [x,t] = λnY αn (x;k)tn,
n=0](a211x.png) | (2) |
the λn≠0 are arbitrary constants, and ζn(y) is a polynomial of degree n in y given
by
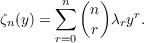 | (3) |
It is also shown that the polynomials Znα(x;k) can be expressed as a finite sum
of Znα(y;k) in the form
![α x-kn∑n ( α+ kn) (kr)! k r α
Z n(x;k) = (y) kr r! [(y∕x) − 1] Zn−r(y;k).
r=0](a213x.png) | (4) |
|





![∑∞ α n − (α+1)∕k −1∕k
Yn (x;k )ζn(y)t = (1− t) exp{x[1 − (1 − t) ]}
n=0
⋅G [x(1 − t)−1∕k,yt∕(1− t)],](a210x.png)
![∑∞
G [x,t] = λnY αn (x;k)tn,
n=0](a211x.png)
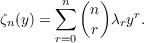
![α x-kn∑n ( α+ kn) (kr)! k r α
Z n(x;k) = (y) kr r! [(y∕x) − 1] Zn−r(y;k).
r=0](a213x.png)
