Isomorphisms of group extensions

Let 0 → G → E → Π → 1 and 0 → G → E′→ Π → 1 be two crossed product extensions given by the crossed product groups E = [G,φ,f,Π] and E′ = [G,φ′,f′,Π] respectively. A homomorphism Γ : E → E′ is stabilizing if the diagram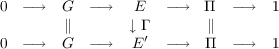

0 −→ G − → E −→ Π −→ 1 ∥ ↓ Γ ∥ 0 −→ G − → E′ −→ Π −→ 1

commutes. In this paper, a necessary and sufficient condition for the existence of a stabilizing homomorphism (hence isomorphism) between any two crossed product extensions is obtained.

The result is applied to obtain a necessary and sufficient condition for the existence of an automorphism Φ : E → E making the diagram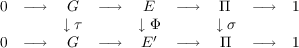

0 −→ G −→ E −→ Π − → 1 ↓ τ ↓ Φ′ ↓ σ 0 −→ G −→ E −→ Π − → 1

commutative, given (σ,τ) ∈ AutΠ × AutG.

Mathematical Subject Classification

Primary: 20F25

Milestones

Received: 28 September 1972

Published: 1 January 1974

Authors

Kung-Wei Yang

Vol. 50, No. 1, 1974

Kung-Wei Yang

Abstract

Mathematical Subject Classification

Milestones

Authors