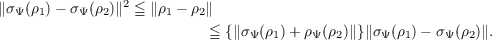|
For a cyclic and separating
vector Ψ of a von Neumann algebra R, the corresponding modular conjugation
operator JΨ is characterized by the property that it is an antiunitary involution
satisfying JΨΨ = Ψ,JΨRJΨ = R′ and (Ψ,QjΨ(Q)Ψ) ≧ 0 for all Q ∈ R where
jΨ(Q) = JΨQJΨ.
The strong closure V Ψ of the vectors QjΨ(Q)Ψ is shown to be a JΨ-invariant
pointed closed convex cone which algebraically span the Hilbert space H. Any
JΨ-invariant Φ ∈ H has a unique decomposition Φ = Φ1 − Φ2 such that Φj ∈ V Ψ and
sR(Φ1) ⊥ sR(Φ2).
There exists a unique bijective homeomorphism σΨ from the set of all normal
linear functionals on R onto V Ψ such that the expectation functional by the vector
σΨ(ρ) is ρ. It satisfies
Any two σΨ and σΨ′ are related by a unitary u′ in R′ by u′σΨ(ρ) = σΨ′(ρ) for all
ρ.
The relation lρ1 ≧ ρ2 holds if and only if there exists A(ρ2∕ρ1) ∈ R such that
A(ρ2∕ρ1)σΨ(ρ1) = σΨ(ρ2). The smallest l is given by ∥A(ρ2∕ρ1)∥. It satisfies
the chain rule A(ρ3∕ρ2)A(ρ2∕ρ1) = A(ρ3∕ρ1). It coincides with the positive
square root of the measure theoretical Radon-Nikodym derivative if R is
commutative.
As an application, it is shown that product of any two modular conjugation jΨjΦ
is an inner automorphism of R.
For a product state ⊗ρj of a C∗ algebra generated by finite W∗ tensor products
{⊗j∈IRj}⊗{⊗j∈I1j} of von Neumman algebras Rj, it is shown that ⊗ρj and ⊗ρj′
are equivalent if and only if Σ∥σΨ(ρj) − σΨ(ρj′)∥2 < ∞ where ∥σΨ(ρ) − σΨ(ρ′)∥ is
independent of Ψ.
It is shown that there exists a unitary representation UΨ(g) of the group
of all ∗-automorphisms of R such that UΨ(g)αjUΨ(g)∗ = g(x) for all
x ∈ R and UΨ(g)σΨ(g∗ρ) = σΨρ for all normal positive linear functionals
ρ.
|