An identity for matrix functions

Russell L. Merris

Vol. 50 (1974), No. 2, 557–562

DOI: 10.2140/pjm.1974.50.557

Abstract

Let G ⊂ S_n. Let η be a character on G. For A = (a_ij) an n-square matrix, define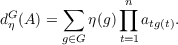

A general identity for idempotents in group algebras is proved. A very special example of the consequences is this: If χ is a linear character on G and H a normal subgroup of G, then [G : H]d_χ^H(A) = ∑ η(1)d_η^G(A), where the summation is over those irreducible characters η of G whose restriction to H contain χ as a component.

Mathematical Subject Classification 2000

Primary: 15A15

Milestones

Received: 4 October 1972

Published: 1 February 1974