|
|||||

|

|
|

|

|
|
Polynomials and
Hausdorff matrices
Philip C. Tonne |
|
Vol. 50 (1974), No. 2, 613–615
|
Abstract |
|
If f is a function from the rational numbers in [0,1] to the complex plane and c is a complex sequence, then the Hausdorff matrix H(c) for c and a sequence L(f,c) are defined: 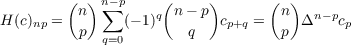
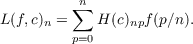
Theorem. If f is a function from the rationals in [0,1] to the plane and L(f,c) converges for each complex sequence c, then f is a subset (contraction) of a polynomial. |
Mathematical Subject Classification 2000
Primary: 41A05
|
Milestones
Received: 12 October 1972
Revised: 26 February 1973
Published: 1 February 1974
|
Authors |
| Philip C. Tonne | |
 |
