Strictly local solutions of Diophantine equations

Marvin J. Greenberg

Vol. 51 (1974), No. 1, 143–153

DOI: 10.2140/pjm.1974.51.143

Abstract

For any system f of Diophantine equations, there exist positive integers C(f),D(f) with the following properties: For any nonnegative integer n, for any prime p, if v is the p-adic valuation, and if a vector x of integers satisfies the inequality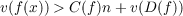

then there is an algebraic p-adic integral solution y to the system f such that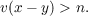

This theorem is proved by techniques of algebraic geometry in the more general setting of Noetherian domains of characteristic zero. When f is just a single equation, the method of Birch and McCann gives an effective determination of C(f) and D(f).

Mathematical Subject Classification

Primary: 10B40

Secondary: 12B05

Milestones

Received: 20 November 1972

Published: 1 March 1974