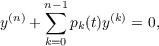|
Consider the n-th order
linear differential equation
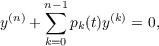 | (1) |
where pk(t) ∈ C[α,∞). This study explores some of the relationships between
multi-point boundary value functions for (1) and the character of oscillatory solutions
of (1). In particular, it is supposed for (1) that a certain (n− 1) point boundary value
problem has no nontrivial solution and that two nontrivial solutions with (n − 1)
zeros in common are constant multiples of each other. Under these conditions it is
shown that there exists an integer i,1 ≦ i ≦ n− 1, such that for each a > α and every
integer l,1 ≦ l ≦ i − 1, there is an oscillatory solution of (1) with a zero of exact
multiplicity l at t = a. Furthermore, any solution of (1) with a zero at t = a of
multiplicity l ≧ i is nonoscillatory.
|