Oscillation and nonoscillation criteria for some self-adjoint even order linear differential operators

Roger T. Lewis

Vol. 51 (1974), No. 1, 221–234

DOI: 10.2140/pjm.1974.51.221

Abstract

Oscillation and nonoscillation results are presented for the operator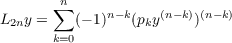

where p₀(x) > 0 on (0,∞) and for k = 0,1,⋯,n,p_k is a realvalued, n − k times differentiable function on (0,∞). Also, y is an element of the set of all real-valued, 2n-fold continuously differentiable, finite functions on (0,∞).

In particular, a nonoscillation result is given for L_2n without sign restrictions on the coefficients. Oscillation results are given for L₄ without the requirement that p₁ be negative for large x. Finally, the oscillation of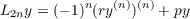

is considered for r(x) not necessarily bounded.

Mathematical Subject Classification 2000

Primary: 34C10

Milestones

Received: 18 December 1972

Revised: 15 June 1973

Published: 1 March 1974