|
Let N be the set of
nonnegative integers, and let B = Σ ⊕ [bi](i ∈ N) be the direct sum of cyclic
groups with 0(bt) = pi+1. Denote by B the torsion-completion of B. This
paper is concerned with pure subgroups of the group B. If G is such a group,
let
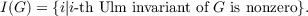
Beaumont and Pierce introduced a further invariant for G, namely,
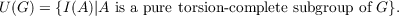
U(G) is a (boolean) ideal in 𝒫(N), the power set of N.
If ℐ is an ideal in 𝒫(N), lhen the canonical example of a pure subgroup, G, of B
with U(G) = ℐ is constructed as follows:
.](a312x.png)
Beaumont and Pierce showed that if 𝒫(N)∕ℐ has no atoms and ℐ is free, then there
exist maximal pure subgroups G of B such that G ⊃𝒢(ℐ) and U(G) = ℐ. The
purpose of this paper is to give necessary and sufficient conditions for the
existence of such a G in the case that 𝒫(N)∕ℐ is finite. In the process, some
information is obtained about the number of nonisomorphic extensions of
𝒢(ℐ).
|




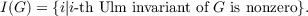
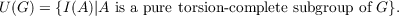
.](a312x.png)

