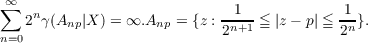|
Let X be a compact plane set.
Denote by R(X) the uniform algebra generated by the rational functions with poles
off X and by H(X) the space of functions harmonic in a neighborhood of X endowed
with the sup norm. A point p ∈ ∂X is a peak point for R(X) if there exists a function
f ∈ R(X) such that f(p) = 1 and |f(x)| < 1 if x≠p. Moreover, p is a peak point for
H(X) (consider Ref) and hence, by a theorem of Keldysh, p is a regular point for the
Dirichlet problem. Conditions which determine whether or not a point is a
peak point for R(X) are thus of interest in harmonic analysis. Melnikov has
given a necessary and sufficient condition that p be a peak point for R(X) in
terms of analytic capacity, γ; namely p is a peak point for R(X) if and only
if
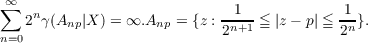
Analytic capacity is generally difficult to compute, so it is desirable to obtain more
computable types of conditions. Let Xc = C|X and I = {t ∈ [0,1] : z ∈ Xc and |z| = t}.
In this note the following conjecture, which can be found in Zalcman’s Springer
Lecture Notes and which is true for certain sets X, is shown to be false in
general:
Conjecture. If ∫
It−1dt = ∞ then 0 is a peak point for R(X).
|