On the eigenvalues of a second order elliptic operator in an unbounded domain

Denton Elwood Hewgill

Vol. 51 (1974), No. 2, 467–476

DOI: 10.2140/pjm.1974.51.467

Abstract

Let E be an open set in Rⁿ which satisfies the “narrowness at infinity” condition: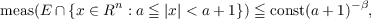

for all a > 0 and some β > 0. It is known that a uniformly strongly elliptic self-adjoint partial differential operator, on such a set E, has a discrete spectrum of eigenvalues {λ_j}. This paper is concerned with the growth rate of the function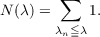

The main result of the paper is to give an upper bound for N(λ). This upper bound will be a function of the β from the “narrowness” condition.

Mathematical Subject Classification 2000

Primary: 35P20

Milestones

Received: 14 February 1973

Revised: 25 June 1973

Published: 1 April 1974