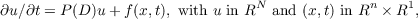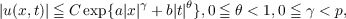|
Hyperbolic systems of N
equations are considered
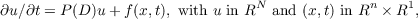 | (1) |
where D = i∂∕∂x. For suitable source functions f(x,t) there are solutions satisfying
the boundedness condition
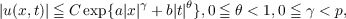 | (2) |
where p is the conjugate of 2p0, with p0 the reduced order of the matrix P(ξ).
Furthermore, the solutions are polynomials in t if the initial states u(x,0) grow at
infinity like polynomials. However, these solutions are not unique; a requirement of a
certain type of u(x,0) at infinity is needed. The one-dimensional classical
Phragmén-Lindelöf theorem and some results of Shilov for homogeneous systems
are instances of this. It is the purpose here to supply a general (necessary and for
some cases sufficient) condition for uniqueness. Preliminary to that a necessary
condition is found on f(x,t) so that (1) admits solutions that are polynomials in
t.
|