On the Nielsen number of a fiber map

Dennis McGavran and Jingyal Pak

Vol. 52 (1974), No. 1, 149–156

DOI: 10.2140/pjm.1974.52.149

Abstract

Suppose 𝒯 = {E,π,B,F} is a fiber space such that 0 → π₁(F) → π₁(E)i_# → π₁(B)π# → 0 is exact. Suppose also that the above fundamental groups are abelian. If f : E → E is a fiber preserving map such that f_$(α) = α if and only if α = 0, then it is shown that R(f) = R(f′) ⋅ R(f_b) where R(h) is the Reidemeister number of the map h.

A product formula for the Nielsen number of a fiber map which holds under certain conditions was introduced by R. Brown. Let 𝒯 = {E,π,L,(p,q),s¹} be a principal s¹-bundle over the lens space L(p,q), where 𝒯 is determined by [f_f] ∈ [L(p,q),cp^∞] ≃ H²(L(p,q),z) ≃ z_p. Let f : E → E be a fiber preserving map such that f_b#(1) = c₂,f_#′(l_p) = c₁, where 1 generates π₁(s¹) ≃ z and l_p generates π₁(L(p,q)) ≃ z_p. Then the Nielsen numbers of the maps involved satisfy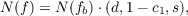

where d = (j,p) and s = j∕p(c₁ − c₂).

Mathematical Subject Classification

Primary: 55C20

Secondary: 55F05

Milestones

Received: 29 August 1973

Published: 1 May 1974