Fundamental groups of compact complete locally affine complex surfaces. II

John Herman Scheuneman

Vol. 52 (1974), No. 2, 553–566

DOI: 10.2140/pjm.1974.52.553

Abstract

The present article is a continuation of a recent paper by J. P. Fillmore and the author on properly-acting groups Γ of complex affine motions of C² such that Γ∖C² is compact. In that paper, it was proved that such a group has a normal subgroup Γ₀ of finite index which is either free abelian of rank four or has generators A,B,C,D, with relations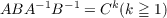

and C and D central.

Here we build on this description up to finite index to determine the groups Γ themselves.

Mathematical Subject Classification 2000

Primary: 32M10

Secondary: 20E40

Milestones

Received: 12 August 1973

Published: 1 June 1974