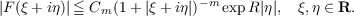|
The classical theorem of
Paley-Wiener is concerned with characterizing Fourier transforms of C∞ functions of
compact support on the real line. It states that an entire holomorphic function F is
the Fourier-Laplace transform of a C∞ function on the real line R with support in
|x|≦ R it and only if for given integer m, there exists a constant Cm such
that
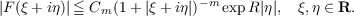 | (1) |
The purpose of this paper is to prove an analogue of this theorem for certain
convolution subalgebras of C∞ functions with compact support on the group
SL(2,C), by using Fourier transform involving elementary spherical functions of
general type δ.
|