A factorization theorem for p-constrained groups

William H. Specht

Vol. 53 (1974), No. 1, 253–258

DOI: 10.2140/pjm.1974.53.253

Abstract

Suppose that G is a finite p-constrained group. For some prime p ≧ 5 let S be a Sylow p-subgroup. Assume that G admits a group of automorphisms A such that (|A|,|G|) = 1 and the fixed point subgroup of A does not involve PSL (2,p). In this paper it is shown that under these conditions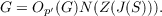

Mathematical Subject Classification 2000

Primary: 20D15

Milestones

Received: 2 March 1973

Published: 1 July 1974