|
A triangle of size n is a
collection {Au} of n(n + 1)∕2 (not necessarily distinct) rank one torsion-free abelian
groups indexed by all integer sequences of the form u = i,i + 1,⋯ , i + j with
1 ≦ i ≦ i + j ≦ n, satisfying T(Au) + T(As) ≦ T(Aus) for all consecutive sequences
u,s. Here T(Av) denotes the type of the rank one torsion-free abelian group Av. If
A = ⊕i∈IAi is a direct sum of rank one torsion-free abelian groups Ai, let
Δ(A) = sup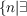 a triangle of size n of groups chosen, possibly with repetitions, from
{Ai|i ∈ I} a triangle of size n of groups chosen, possibly with repetitions, from
{Ai|i ∈ I}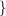 , Δ′(A) = sup , Δ′(A) = sup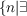 a triangle of size n of groups chosen without
repetition from {Ai|i ∈ I} a triangle of size n of groups chosen without
repetition from {Ai|i ∈ I}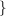 . An abelian group (G,+) is radical iff whenever
(R,+,⋅) is a ring with (R,+)≅(G,+) there exists a positive integer n with
Rn = (0). . An abelian group (G,+) is radical iff whenever
(R,+,⋅) is a ring with (R,+)≅(G,+) there exists a positive integer n with
Rn = (0).
|





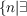 a triangle of size
a triangle of size 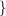 ,
, 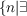 a triangle of size
a triangle of size 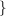 . An abelian group
. An abelian group 