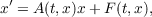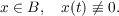Nonzero solutions to boundary value problems for nonlinear systems

Athanassios G. Kartsatos

Vol. 53 (1974), No. 2, 425–433

DOI: 10.2140/pjm.1974.53.425

Abstract

We are mainly concerned here with solutions of

(*)

which satisfy the following conditions

(1.1)

Here A(t,u) is a real n×n matrix defined and continuous on J ×Rⁿ, where J is a subinterval of R = (−∞,∞). The real n-vector F(t,u) is also defined and continuous on J × Rⁿ. In (1.1) B is a Banach space of continuous functions on J.

Mathematical Subject Classification 2000

Primary: 34B15

Milestones

Received: 16 March 1973

Published: 1 August 1974