Arithmetic properties of certain recursively defined sets

David Anthony Klarner and R. Rado

Vol. 53 (1974), No. 2, 445–463

DOI: 10.2140/pjm.1974.53.445

Abstract

Let R denote a set of linear operations defined on the set N of nonnegative integers; for example, a typical element of R has t he form ρ(x₁,⋯,x_r) = m₀ + m₁x₁ + ⋯ + m_rx_r where m₀,⋯,m_r denote certain integers. Given a set A of positive integers, there is a smallest set of positive integers denoted ⟨R : A⟩ which contains A as a subset and is closed under every operation in R. The set ⟨R : A⟩ can be constructed recursively as follows: Let A₀ = A, and define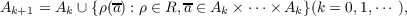

then it can be shown that ⟨R : A⟩ = A₀ ∪ A₁ ∪⋯ . The sets ⟨R : A⟩ sometimes have an elegant form, for example, the set ⟨2x + 3y : 1⟩ consists of all positive numbers congruent to 1 or 5 modulo 12. The objective is to give an arithmetic characterization of elements of a set ⟨R : A⟩. This paper is a report on progress made on this problem when the authors collaborated at Reading University in the academic year 1970–71.

Mathematical Subject Classification 2000

Primary: 10A99

Secondary: 05B10, 04A05

Milestones

Received: 29 November 1972

Revised: 21 January 1974

Published: 1 August 1974