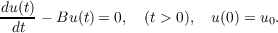Existence, uniqueness and limiting behavior of solutions of a class of differential equations in Banach space

John Lagnese

Vol. 53 (1974), No. 2, 473–485

DOI: 10.2140/pjm.1974.53.473

Abstract

Let X be a Banach space (real or complex) and A_n and B be linear operators in X with D(B) ⊆ D(A_n),n = 1,2,⋯ . The following note is concerned with existence and uniqueness of solutions of the problem

(1.1)

and the limiting behavior of these solutions as the operators A_n tend to zero in a sense to be specified. We will show that for a large class of operators the problem (1.1) is well posed and that its solutions tend to the solution of the problem

(1.2)

Mathematical Subject Classification 2000

Primary: 34G05

Secondary: 35L99

Milestones

Received: 30 May 1972

Revised: 20 February 1973

Published: 1 August 1974