Fixed points and characterizations of certain maps

Chi Song Wong

Vol. 54 (1974), No. 1, 305–312

DOI: 10.2140/pjm.1974.54.305

Abstract

Let T be a self map on a metric space (X, d) such that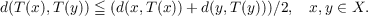

It is proved that: (a) T has a fixed point if T is continuous and X is weakly compact convex subset of a Banach space. (b) All such T which have fixed points can be explicitly determined in terms of d. Related results are obtained.

Mathematical Subject Classification 2000

Primary: 47H10

Milestones

Received: 28 March 1973

Published: 1 September 1974