|
An entire function f(z) is said
Co have bounded value distribution (b.v.d.) if there exist constants p, R such that
the equation f(z) = w never has more than p roots in any disk of radius
R. It was shown by W. K. Hayman that this is the case for a particular p
and some R > 0 if and only if there is a constant C > 0 such that for all
z
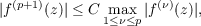
so that f′(z) has bounded index in the sense of Lepson.
The fact that f′(z) has bounded index if f(z) has b.v.d. follows readily from a
classical result on p-valent functions. In the other direction Hayman proved that
if
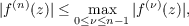
then f(z) cannot have more than n − 1 zeros in |z|≤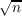 ∕e ∕e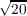 . Here the order of
magnitude is correct in the sense that . Here the order of
magnitude is correct in the sense that 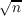 ∕e ∕e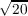 cannot be replaced by cannot be replaced by 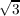 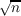 . The
result when applied to f(z) − w does show that f′(z) has bounded index only
iff(z) has b.v.4. but it is clearly of interest to determine the largest disk
containing at most n − 1 zeros of f(z). We are able to replace . The
result when applied to f(z) − w does show that f′(z) has bounded index only
iff(z) has b.v.4. but it is clearly of interest to determine the largest disk
containing at most n − 1 zeros of f(z). We are able to replace 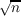 ∕e ∕e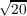 by by
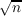 ∕e ∕e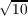 . .
|




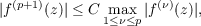
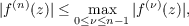

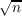
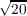 . Here the order of
magnitude is correct in the sense that
. Here the order of
magnitude is correct in the sense that 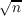
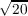 cannot be replaced by
cannot be replaced by 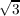
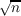 . The
result when applied to
. The
result when applied to 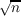
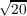 by
by
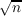
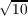 .
.