|
Let H be the Hilbert space of
complex vector-valued functions f :  a,∞ a,∞ → C2 such that f is Lebesgue
measurable on → C2 such that f is Lebesgue
measurable on  a,∞ a,∞ and ∫
a∞f∗(s)f(s)ds < ∞. Consider the formally self adjoint
expression c(y) = −y′′ + Py on and ∫
a∞f∗(s)f(s)ds < ∞. Consider the formally self adjoint
expression c(y) = −y′′ + Py on  a,∞ a,∞ , where y is a 2-vector and P is a 2 × 2
symmetric matrix of continuous real valued functions on , where y is a 2-vector and P is a 2 × 2
symmetric matrix of continuous real valued functions on  a,∞ a,∞ . Let D be the linear
manifold in H defined by . Let D be the linear
manifold in H defined by
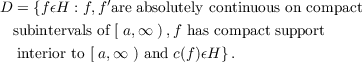
Then the operator L defined by L(y) = f(y),y𝜖D, is a real symmetric operator on
D. Let L0 be the minimal closed extension of L. For this class of minimal
closed symmetric operators this paper determines sufficient conditions for the
continuous spectrum of self adjoint extensions to be the entire real axis.
Since the domain, D0, of L0 is dense in H, self adjoint extensions of L0 do
exist.
|




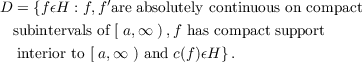




 and
and 
 , where
, where 
 . Let
. Let 